Publications
2024
-
-
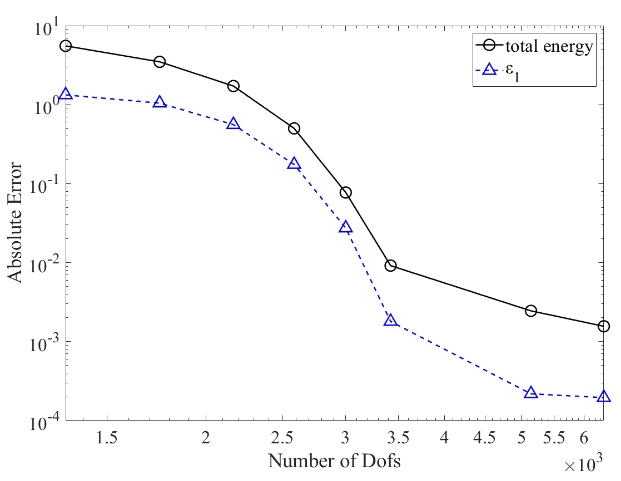
A hierarchical splines-based h-adaptive isogeometric solver for all-electron Kohn--Sham equation
Tao Wang, Yang Kuang*, Ran Zhang, Guanghui Hu
(2024)
ABSTRACT BIB
In this paper, a novel h-adaptive isogeometric solver utilizing high-order hierarchical splines is proposed to solve the all-electron Kohn--Sham equation. In virtue of the smooth nature of Kohn--Sham wavefunctions across the domain, except at the nuclear positions, high-order globally regular basis functions such as B-splines are well suited for achieving high accuracy. To further handle the singularities in the external potential at the nuclear positions, an h-adaptive framework based on the hierarchical splines is presented with a specially designed residual-type error indicator, allowing for different resolutions on the domain. The generalized eigenvalue problem raising from the discretized Kohn--Sham equation is effectively solved by the locally optimal block preconditioned conjugate gradient (LOBPCG) method with an elliptic preconditioner, and it is found that the eigensolver's convergence is independent of the spline basis order. A series of numerical experiments confirm the effectiveness of the h-adaptive framework, with a notable experiment that the numerical accuracy 0.001 Hartree/particle in the all-electron simulation of a methane molecule is achieved using only 6355 degrees of freedom, demonstrating the competitiveness of our solver for the all-electron Kohn--Sham equation.
-

-
A high-order accurate moving mesh finite element method for the radial Kohn--Sham equation
Zheming Luo, Yang Kuang*
(2024)
ABSTRACT BIB
In this paper, we introduce a highly accurate and efficient numerical solver for the radial Kohn--Sham equation. The equation is discretized using an up to 10-th order finite element method, with its performance further improved by incorporating a parameter-free moving mesh technique. This approach greatly reduces the number of elements required to achieve the desired precision. In practice, the mesh redistribution involves no more than three steps, ensuring the algorithm remains computationally efficient. Remarkably, with a maximum of 13 elements, we successfully reproduce the NIST database results for elements with atomic numbers ranging from 1 to 92.
-
-
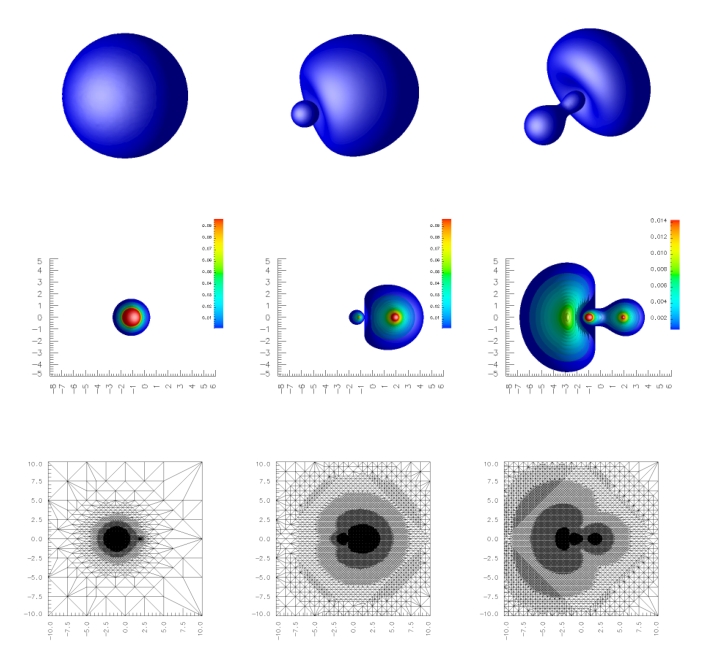
A novel splitting strategy to accelerate solving generalized eigenvalue problem from Kohn--Sham density functional theory
Yang Kuang, Guanghui Hu
(2024)
ABSTRACT BIB
In this paper, we propose a novel eigenpair-splitting method, inspired by the divide-and-conquer strategy, for solving the generalized eigenvalue problem arising from the Kohn-Sham equation. Unlike the commonly used domain decomposition approach in divide-and-conquer, which solves the problem on a series of subdomains, our eigenpair-splitting method focuses on solving a series of subequations defined on the entire domain. This method is realized through the integration of two key techniques: a multi-mesh technique for generating approximate spaces for the subequations, and a soft-locking technique that allows for the independent solution of eigenpairs. Numerical experiments show that the proposed eigenpair-splitting method can dramatically enhance simulation efficiency, and its potential towards practical applications is also demonstrated well through an example of the HOMO-LUMO gap calculation. Furthermore, the optimal strategy for grouping eigenpairs is discussed, and the possible improvements to the proposed method are also outlined.
-

-
Towards chemical accuracy using a multi-mesh adaptive finite element method in all-electron density functional theory
Yang Kuang, Yedan Shen, Guanghui Hu
Journal of Computational Physics, 518, 113321 (2024)
ABSTRACT BIB
Chemical accuracy serves as an important metric for assessing the effectiveness of the numerical method in Kohn--Sham density functional theory. It is found that to achieve chemical accuracy, not only the Kohn--Sham wavefunctions but also the Hartree potential, should be approximated accurately. Under the adaptive finite element framework, this can be implemented by constructing the a posteriori error indicator based on approximations of the aforementioned two quantities. However, this way results in a large amount of computational cost. To reduce the computational cost, we propose a novel multi-mesh adaptive method, in which the Kohn--Sham equation and the Poisson equation are solved in two different meshes on the same computational domain, respectively. With the proposed method, chemical accuracy can be achieved with less computational consumption compared with the adaptive method on a single mesh, as demonstrated in a number of numerical experiments.
2022
-
-
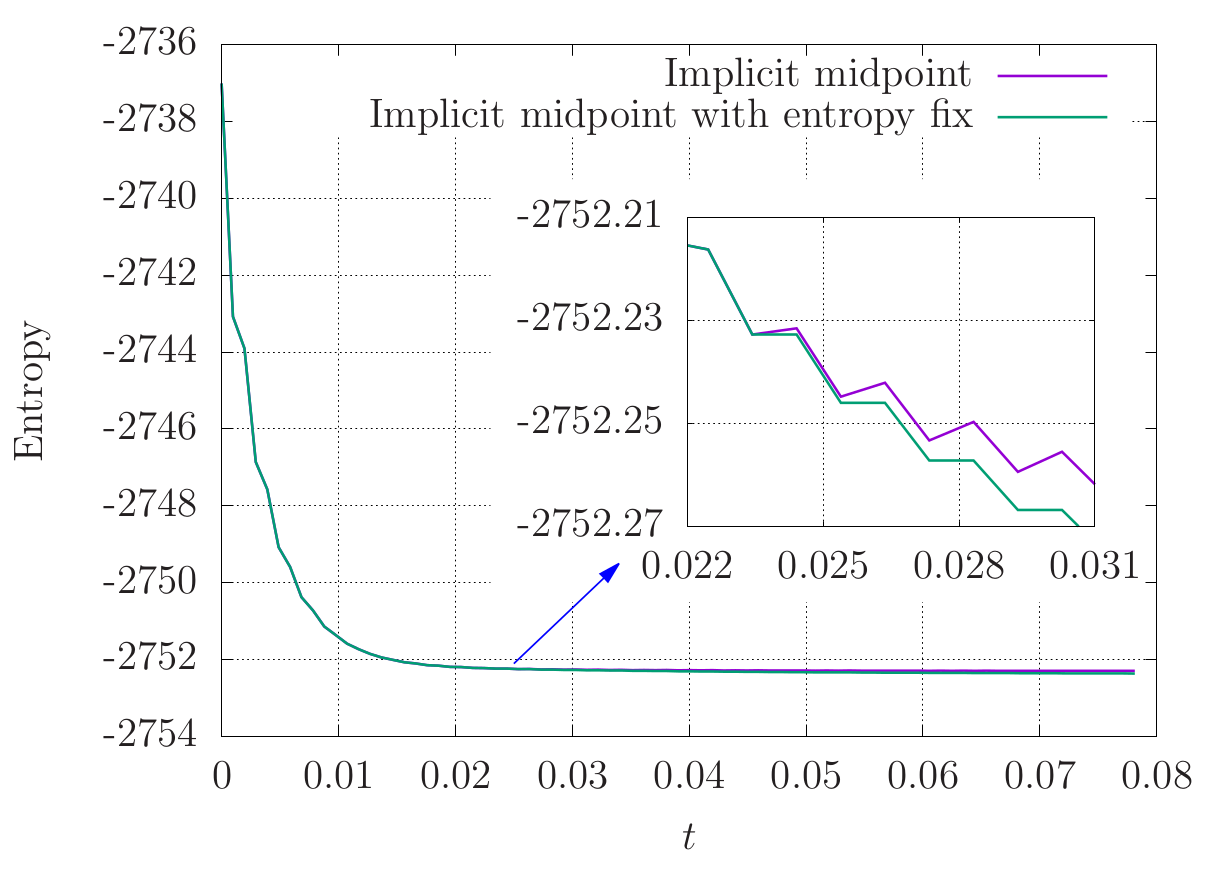
An entropic method for discrete systems with Gibbs entropy
Zhenning Cai, Jingwei Hu, Yang Kuang, Bo Lin
SIAM Journal on Numerical Analysis, 60 (4), 2345-2371 (2022)
ABSTRACT BIB
We consider general systems of ordinary differential equations with monotonic Gibbs entropy, and introduce an entropic scheme that simply imposes an entropy fix after every time step of any existing time integrator. It is proved that in the general case, our entropy fix has only infinitesimal influence on the numerical order of the original scheme, and in many circumstances, it can be shown that the scheme does not affect the numerical order. Numerical experiments on the linear Fokker-Planck equation and nonlinear Boltzmann equation are carried out to support our numerical analysis.
-

-
An orthogonalization-free parallelizable framework for all-electron calculations in density functional theory
Bin Gao, Guanghui Hu, Yang Kuang*, Xin Liu
SIAM Journal on Scientific Computing, 44 (3), B723-B745 (2022)
ABSTRACT BIB
All-electron calculations play an important role in density functional theory, in which improving computational efficiency is one of the most needed and challenging tasks. In the model formulations, both the nonlinear eigenvalue problem and the total energy minimization problem pursue orthogonal solutions. Most existing algorithms for solving these two models invoke orthogonalization process either explicitly or implicitly in each iteration. Their efficiency suffers from this process in view of its cubic complexity and low parallel scalability in terms of the number of electrons for large scale systems. To break through this bottleneck, we propose an orthogonalization-free algorithm framework based on the total energy minimization problem. It is shown that the desired orthogonality can be gradually achieved without invoking orthogonalization in each iteration. Moreover, this framework fully consists of BLAS operations and thus can be naturally parallelized. The global convergence of the proposed algorithm is established. We also present a preconditioning technique which can dramatically accelerate the convergence of the algorithm. The numerical experiments on all-electron calculations show the effectiveness and high scalability of the proposed algorithm.
-

-
Regularization of the complex Langevin method
Zhenning Cai, Yang Kuang*, Hong Kiat Tan
Physical Review D, 105 (1), 014508 (2022)
ABSTRACT BIB
The complex Langevin method, a numerical method used to compute the ensemble average with a complex partition function, often suffers from runaway instability. We study the regularization of the complex Langevin method via augmenting the action with a stabilization term. Since the regularization introduces biases to the numerical result, two approaches, named 2R and 3R methods, are introduced to recover the unbiased result. The 2R method supplements the regularization with regression to estimate the unregularized ensemble average, and the 3R method reduces the computational cost by coupling the regularization with a reweighting strategy before regression. Both methods can be generalized to the SU(n) theory and are assessed from several perspectives. Several numerical experiments in the lattice field theory are carried out to show the effectiveness of our approaches.
2021
-

-
An h-adaptive finite element method for Kohn-Sham and time-dependent Kohn-Sham equations
Yang Kuang, Yedan Shen, Guanghui Hu
Journal on Numerica Methods and Computer Applications, 42 (1), 33 (2021)
ABSTRACT BIB
Quality numerical simulations of the dynamics of a given many-body electronic structure system is an important research area in material analysis and nano-optics, etc. Quantities such as the time-dependent dipole moment are essential for further study. There are two components in such simulations, i.e., the ground state calculation, and the following dynamic simulations with the ground state as an initial state. These two components can be obtained by solving Kohn-Sham and time-dependent Kohn-Sham equations, respectively. In this paper, based on the finite element method, a unified numerical framework is proposed for the whole simulation. For the ground state calculation, the classical self-consistent field iteration method is employed for the linearization of the equation, in which the derived generalized eigenvalue problem is solved by the locally optimal blocked preconditioned conjugate gradient method, and we also design an effective preconditioner based on the multigrid method for the acceleration of the iteration. For the simulation of the dynamics, an implicit midpoint scheme is used for the temporal discretization, while the linear finite element method is used for the spatial discretization. A predictor-corrector method is used for the linearization of the equation, and an algebraic multigrid solver is developed for the derived complexvalued system in order to accelerate the simulation. In particular, an h-adaptive finite element method is developed for further improving the efficiency, in which two residual type a posteriori error indicators are designed for the Kohn-Sham and time-dependent Kohn- Sham equations, respectively. A variety of numerical experiments verify the effectiveness of our method.
-

-
On the validity of complex Langevin method for path integral computations
Zhenning Cai, Xiaoyu Dong, Yang Kuang
SIAM Journal on Scientific Computing, 43 (1), A685-A719 (2021)
ABSTRACT BIB
The complex Langevin (CL) method is a classical numerical strategy to alleviate the numerical sign problem in the computation of lattice field theories. Mathematically, it is a simple numerical tool to compute a wide class of high-dimensional and oscillatory integrals. However, it is often observed that the CL method converges but the limiting result is incorrect. The literature has several unclear or even conflicting statements, making the method look mysterious. By an in-depth analysis of a model problem, we reveal the mechanism of how the CL result turns biased as the parameter changes, and it is demonstrated that such a transition is difficult to capture. Our analysis also shows that the method works for any observables only if the probability density function generated by the CL process is localized. To generalize such observations to lattice field theories, we formulate the CL method on general groups using rigorous mathematical languages for the first time, and we demonstrate that such localized probability density function does not exist in the simulation of lattice field theories for general compact groups, which explains the unstable behavior of the CL method. Fortunately, we also find that the gauge cooling technique creates additional velocity that helps confine the samples, so that we can still see localized probability density functions in certain cases. Thereby, the gauge cooling method significantly broadens the application of the CL method. The limitations of gauge cooling are also discussed. In particular, we prove that gauge cooling has no effect for Abelian groups, and we provide an example showing that biased results still exist when gauge cooling is insufficient to confine the probability density function.
2020
-

-
On stabilizing and accelerating SCF using ITP in solving Kohn–Sham equation
Yang Kuang, Guanghui Hu
Communications in Computational Physics, 28 (3), 999-1018 (2020)
ABSTRACT BIB
It is found that imaginary time propagation method can effectively deliver a convergent result in solving Kohn–Sham equation, but a sufficient long simulation is needed to reach an accurate enough result, while the self-consistent field iteration method for Kohn–Sham equation can be more efficient when it works, but it sometimes suffers from divergence. In this work, we take advantage of the convergence of imaginary time propagation method by generating a quality initial guess to improve the behavior of self-consistent field iteration. A number of numerical experiments successfully show that i). for those self-consistent field iterations which are sensitive to the initial guess, the results obtained from imaginary time propagation method make the iterations converge, and ii). generally, the convergence of self-consistent field iteration can be accelerated by imaginary time propagation method. It is shown that all-electron models can be resolved well with the proposed method.
2019
-

-
An asymptotics-based adaptive finite element method for Kohn–Sham equation
Yedan Shen, Yang Kuang, Guanghui Hu
Journal of Scientific Computing, 79 (1), 464-492 (2019)
ABSTRACT BIB
In Radovitzky and Ortiz (Comput Methods Appl Mech Eng 172(1–4):203–240, 1999), an error estimation technique for nonlinear PDEs is presented to adaptively generating mesh, based on the reduction of the order of the approximate polynomial. In this paper, following a similar analysis framework, we propose an a posteriori error estimation for Kohn–Sham equation by coarsening mesh. An upper bound for the difference of the total energies on two successively refined meshes is derived by the numerical solutions on two meshes through an asymptotic analysis, which finally generates an a posteriori error estimation. A variety of numerical tests show that such an a posteriori error estimation works very well in our h-adaptive finite element method framework. In addition, to further improve the efficiency, we solve a Poisson equation instead of the Kohn–Sham equation on the coarsened mesh. The effectiveness of this improvement is analyzed and numerically examined.
2018
-
-
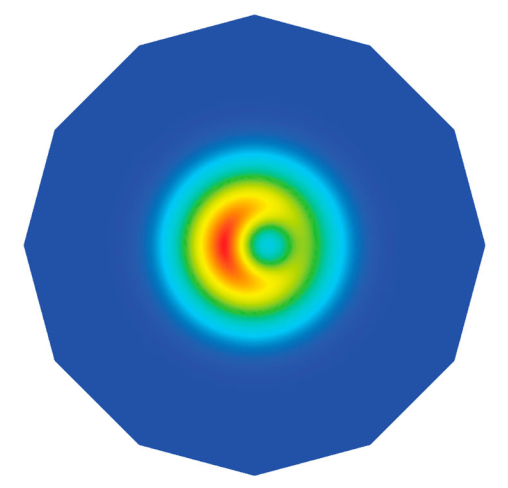
An adaptive FEM with ITP approach for steady Schrödinger equation
Yang Kuang, Guanghui Hu
International Journal of Computer Mathematics, 95 (1), 187-201 (2018)
ABSTRACT BIB
In this paper, an adaptive numerical method is proposed for solving a 2D Schrödinger equation with an imaginary time propagation approach. The differential equation is first transferred via a Wick rotation to a real time-dependent equation, whose solution corresponds to the ground state of a given system when time approaches infinity. The temporal equation is then discretized spatially via a finite element method, and temporally utilizing a Crank–Nicolson scheme. A moving mesh strategy based on harmonic maps is considered to eliminate possible singular behaviour of the solution. Several linear and nonlinear examples are tested by using our method. The experiments demonstrate clearly that our method provides an effective way to locate the ground state of the equations through underlying eigenvalue problems.
* Corresponding author.